Неш-равновесие в торговле: поиск стабильности в рыночной стратегии

В торговле успех часто зависит от предсказания действий других участников рынка. Одной из мощных концепций, которую трейдеры могут использовать для навигации в этих динамиках, является равновесие Нэша — принцип теории игр, при котором стратегия каждого участника является оптимальной с учетом выборов других. Для трейдеров равновесие Нэша может помочь объяснить, как устанавливаются цены, почему определенные сделки остаются стабильными и как совершать действия, которые предвосхищают реакции рынка.

Рассмотрим, как это происходит: когда трейдеры принимают решения, например, устанавливают цены на покупку или продажу, они часто реагируют на или предсказывают, что могут сделать другие. Равновесие Нэша описывает момент, когда ни один отдельный трейдер не может улучшить свой результат, изменяя свою позицию в одиночку. Эта концепция позволяет трейдерам лучше понимать точки баланса на рынке, помогая им ориентироваться в нестабильных рынках, оценивать риски и идентифицировать стабильные точки входа или выхода. В этой статье мы рассмотрим, как равновесие Нэша может быть практически применено к торговым стратегиям, с примерами, которые показывают эту теорию в контексте реальной торговли.

Равновесие Нэша вкратце

Равновесие Нэша, названное в честь математика Джона Нэша, является ключевым понятием в теории игр, которое описывает ситуацию, в которой каждый игрок в "игре" выбирает наилучшую стратегию, исходя из стратегий, выбранных другими. В этот момент ни один игрок не может улучшить свою позицию, изменив только свою стратегию — выборы всех находятся в равновесии.

Равновесие Нэша в теории игр

В теории игр равновесие Нэша — это точка, в которой стратегии всех игроков стабилизируются, так как каждый человек принимает лучшее решение, основываясь на том, что он знает о других. Эта концепция широко используется для прогнозирования поведения в конкурентных сценариях, где результаты зависят от действий нескольких участников, таких как в бизнесе, экономике и, конечно, торговле. Равновесие помогает моделировать ситуации, в которых каждый игрок должен учитывать стратегии других, чтобы принять наилучшее возможное решение.

Примеры для иллюстрации концепции в торговле

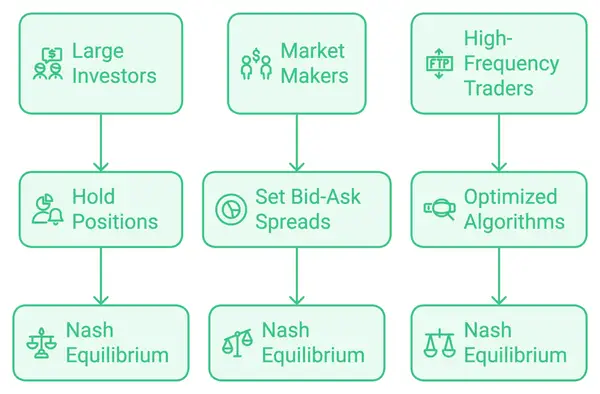
Равновесие Нэша играет важную роль в торговле, где участники принимают стратегические решения, основываясь на ожидаемых действиях других. Вот три примера, которые показывают, как равновесие Нэша применяется в торговых сценариях:

1. Крупные инвесторы и стабильность цен:
   Представьте себе двух крупных инвесторов, владеющих значительными позициями в определенной акции. Каждый из них знает, что продажа большой части своих активов, вероятно, приведет к снижению цены акции, что отразится на их прибыли. Однако если оба трейдера удерживают свои позиции, они сохраняют стоимость акций и избегают убытков.

   Равновесие Нэша: В этом случае оба трейдера достигают стабильного результата, удерживая свои позиции. Если один продает, а другой удерживает, продавец может столкнуться со снижением цены на свои акции. В точке равновесия ни один трейдер не имеет стимула изменять свою стратегию независимо, поскольку это приведет к снижению их общей прибыли.

2. Маркетмейкеры устанавливают спреды:
   Маркетмейкеры отвечают за установление цен на покупку (bid) и продажу (ask) на рынке. Два конкурирующих маркетмейкера для одного и того же актива должны решить, какой спред установить, балансируя между прибылью и объемом торгов. Если один из них сужает спред, он может привлечь больше трейдеров, но потеряет в прибыли. Если оба держат спреды широкими, объем торгов может снизиться из-за более высоких затрат для трейдеров.

   Равновесие Нэша: Равновесие достигается, когда оба маркетмейкера устанавливают аналогичные спреды, которые максимизируют прибыль, не жертвуя слишком большим объемом. Ни один из них не может улучшить свою позицию в одиночку, не заставляя другого реагировать, что вернет их в сбалансированное состояние. Этот стабильный спред выгоден для обоих, предотвращая ценовую войну, которая сократила бы прибыль.

3. Высокочастотная торговля и тайминг ордеров:
   Высокочастотные трейдеры (HFT) часто конкурируют за выполнение ордеров за миллисекунды, чтобы извлечь выгоду из небольших колебаний цен. В этом конкурентном пространстве алгоритмы каждого трейдера разработаны для мгновенной реакции на действия других. Если одна HFT-компания пытается замедлиться для повышения точности, она рискует потерять прибыльные сделки более быстрым конкурентам.

   Равновесие Нэша: Равновесие достигается, когда все компании используют аналогично оптимизированные алгоритмы, которые максимизируют скорость без ущерба для прибыльности. Ни одна отдельная HFT-компания не сможет выиграть, замедлившись или изменив свой подход, так как она потеряет позиции по сравнению с конкурентами. Результатом является стабильная, динамичная среда, где стратегия каждой компании формируется действиями других.

Применение равновесия Нэша в торговле

Равновесие Нэша помогает трейдерам понять стабильные точки на рынке, где никто не может улучшить свой результат в одиночку, предоставляя ценные идеи для стратегии. Вот несколько практических применений:

• Идентификация уровней поддержки и сопротивления: На рынках с крупными игроками равновесие Нэша может помочь предсказать стабильные ценовые уровни, где крупные участники вряд ли изменят свои позиции. Это может выделить вероятные точки поддержки или сопротивления, помогая трейдерам более эффективно устанавливать цены для входа и выхода.

• Оптимизация размеров сделок: Понимая равновесие, трейдеры могут избегать крупных сделок, которые могут нарушить цены и вызвать реакции. Меньшие, поэтапные ордера помогают трейдерам достигать лучших цен без привлечения внимания со стороны других участников рынка.

• Навигация по спредам маркетмейкеров: Маркетмейкеры устанавливают спреды бид-аск на уровнях равновесия, чтобы сбалансировать объем торгов и прибыль. Признавая эти спредовые модели, трейдеры могут лучше выбирать время для своих ордеров, когда цены стабильны.

• Предсказание движений высокой частоты: На быстро меняющихся рынках трейдеры высокой частоты быстро реагируют друг на друга, создавая ценовую стабильность в узких диапазонах. Наблюдение за этими точками равновесия может помочь трейдерам выбрать время для сделок на высоколиквидных рынках.

Использование равновесия Нэша в торговле может выявить точки стабильности, помогая трейдерам предсказывать ценовые уровни и оптимизировать стратегии, которые соответствуют более широкому поведению рынка.

Часто задаваемые вопросы

Что такое равновесие Нэша в торговле?

Равновесие Нэша в торговле описывает точку, в которой стратегии трейдеров стабилизируются, потому что никто не может получить выгоду, изменяя свой подход в одиночку, учитывая стратегии других. Это помогает объяснить стабильные уровни цен и торговое поведение на конкурентных рынках.

Как можно использовать равновесие Нэша в торговле?

Трейдеры используют равновесие Нэша для предсказания точек стабильности на рынке, таких как уровни поддержки и сопротивления, где стратегии крупных игроков уравновешиваются. Признание этих точек может помочь трейдерам устанавливать более эффективные цены входа и выхода и избегать действий, которые могут нарушить рынок.

Применимо ли равновесие Нэша в сценариях реальной торговли?

Да, равновесие Нэша применяется в реальной торговле, особенно на рынках с высоким объемом, где трейдеры постоянно реагируют на действия друг друга. Однако важно учитывать такие факторы, как рыночные настроения и внешние влияния, которые могут воздействовать на точки равновесия.

Существуют ли альтернативы равновесию Нэша в торговом анализе?

Другие подходы, такие как поведенческая теория игр и эволюционная теория игр, предлагают понимание торговых сценариев, где эмоции, тренды или развивающиеся стратегии играют роль. Эти подходы могут дополнять равновесие Нэша, добавляя контекст к рыночному поведению, которое может не строго следовать стабильным паттернам равновесия.

Почему понимание равновесия Нэша полезно для трейдеров?

Освоение равновесия Нэша помогает трейдерам принимать обоснованные решения, определяя стабильные уровни цен, синхронизируя сделки с рыночными тенденциями и минимизируя разрушительные стратегии. Это знание может повысить способность трейдера эффективно ориентироваться в конкурентных и быстро меняющихся рынках.

Понимание равновесия Нэша может дать трейдерам стратегическое преимущество, помогая им предвидеть стабильные уровни цен и оптимизировать точки входа и выхода. Платформа Morpher предлагает функции, соответствующие этому подходу, позволяя трейдерам максимально использовать рыночные инсайты. С помощью данных рынка в реальном времени, современных инструментов графиков и торговли без комиссий, Morpher дает вам возможность исследовать стратегии, основанные на равновесии, без типичных затрат, которые могут сократить прибыль.

Готовы применить эти инсайты на практике? Начните торговать на Morpher сегодня и воспользуйтесь платформой, разработанной для поддержки стратегических торговых решений.

Отказ от ответственности: Все инвестиции связаны с риском, и прошлые результаты ценных бумаг, отраслей, секторов, рынков, финансовых продуктов, торговых стратегий или индивидуальной торговли не гарантируют будущих результатов или доходов. Инвесторы несут полную ответственность за любые инвестиционные решения, которые они принимают. Такие решения должны основываться исключительно на оценке их финансового положения, инвестиционных целей, толерантности к риску и потребностей в ликвидности. Этот пост не является инвестиционным советом.