Nash-Gleichgewicht im Handel: Stabilität in der Marktstrategie finden

Im Handel hängt der Erfolg oft davon ab, die Handlungen anderer Marktteilnehmer vorherzusagen. Ein kraftvolles Konzept, das Händler nutzen können, um diese Dynamiken zu navigieren, ist das Nash-Gleichgewicht, ein Prinzip der Spieltheorie, bei dem die Strategie jedes Teilnehmers optimal ist, gegeben die Entscheidungen der anderen. Für Händler kann das Nash-Gleichgewicht helfen zu erklären, wie sich Preise stabilisieren, warum bestimmte Geschäfte stabil bleiben und wie man Bewegungen vornimmt, die auf Marktreaktionen anticipieren.

Betrachten Sie, wie es sich entfaltet: Wenn Händler Entscheidungen treffen, wie das Festlegen von Kauf- oder Verkaufspreisen, reagieren sie oft auf das, was andere als Nächstes tun könnten, oder versuchen, dies vorherzusagen. Das Nash-Gleichgewicht beschreibt den Moment, in dem kein einzelner Händler sein Ergebnis verbessern kann, indem er seine Position allein ändert. Dieses Konzept ermöglicht es Händlern, die Gleichgewichtspunkte des Marktes besser zu verstehen, was ihnen hilft, volatile Märkte zu navigieren, Risiken zu bewerten und stabile Ein- oder Ausstiegspunkte zu identifizieren. In diesem Artikel werden wir untersuchen, wie das Nash-Gleichgewicht praktisch auf Handelsstrategien angewendet werden kann, mit Beispielen, die diese Theorie in einen realen Handelskontext bringen.

Nash-Gleichgewicht in Kürze

Das Nash-Gleichgewicht, benannt nach dem Mathematiker John Nash, ist ein zentrales Konzept der Spieltheorie, das eine Situation beschreibt, in der jeder Spieler in einem „Spiel“ die beste Strategie wählt, die ihm möglich ist, basierend auf den Strategien, die von anderen gewählt wurden. An diesem Punkt kann kein Spieler seine Position verbessern, indem er allein seine eigene Strategie ändert – die Entscheidungen aller sind im Gleichgewicht.

Nash-Gleichgewicht in der Spieltheorie

In der Spieltheorie ist das Nash-Gleichgewicht der Punkt, an dem sich die Strategien aller Spieler stabilisieren, da jeder die beste Entscheidung basierend auf dem trifft, was er über die anderen weiß. Dieses Konzept wird häufig verwendet, um das Verhalten in wettbewerbsintensiven Szenarien vorherzusagen, in denen die Ergebnisse von den Handlungen mehrerer Teilnehmer abhängen, wie zum Beispiel in der Wirtschaft, den Finanzen und natürlich im Handel. Das Gleichgewicht hilft, Situationen zu modellieren, in denen jeder Spieler die Strategien der anderen berücksichtigen muss, um die bestmögliche Entscheidung zu treffen.

Beispiele zur Veranschaulichung des Konzepts im Handel

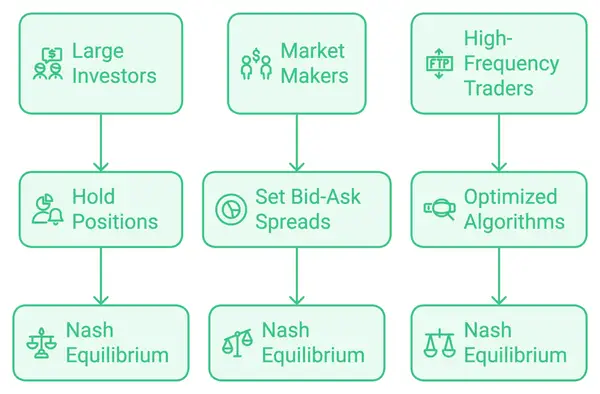
Das Nash-Gleichgewicht spielt eine entscheidende Rolle im Handel, wo Teilnehmer strategische Entscheidungen basierend auf den erwarteten Bewegungen anderer treffen. Hier sind drei Beispiele, die zeigen, wie das Nash-Gleichgewicht in Handelsszenarien angewendet wird:

1. Große Investoren und Preisstabilität:
   Stellen Sie sich zwei große Investoren vor, die erhebliche Positionen in einer bestimmten Aktie halten. Jeder weiß, dass der Verkauf eines großen Teils seiner Bestände wahrscheinlich den Aktienkurs drücken würde, was sich negativ auf ihre Gewinne auswirken könnte. Wenn jedoch beide Händler ihre Positionen halten, bewahren sie den Wert der Aktie und vermeiden einen Verlust.

   Nash-Gleichgewicht: In diesem Fall erreichen beide Händler ein stabiles Ergebnis, indem sie ihre Positionen halten. Wenn einer verkauft, während der andere hält, könnte der Verkäufer einen Preisverfall bei seinen Aktien erleben. Am Gleichgewichtspunkt hat keiner der Händler einen Anreiz, seine Strategie unabhängig zu ändern, da dies ihre Gesamtgewinne verringern würde.

2. Market Maker und Festlegung von Geld-Brief-Spannen:
   Market Maker sind dafür verantwortlich, die Geld- (Kauf) und Briefpreise (Verkauf) im Markt festzulegen. Zwei konkurrierende Market Maker für dasselbe Asset müssen über ihre Spanne entscheiden, wobei sie Gewinnmargen und Handelsvolumen abwägen. Wenn einer die Spanne verringert, könnte er mehr Händler anziehen, jedoch auf Kosten der Gewinne. Wenn beide die Spannen weit halten, könnte das Handelsvolumen aufgrund höherer Kosten für die Händler sinken.

   Nash-Gleichgewicht: Das Gleichgewicht tritt ein, wenn beide Market Maker ähnliche Geld-Brief-Spannen festlegen, die den Gewinn maximieren, ohne zu viel Volumen zu opfern. Keiner kann seine Position allein verbessern, ohne eine Reaktion des anderen hervorzurufen, was sie in einen ausgeglichenen Zustand zurückführen würde. Diese stabile Spanne kommt beiden zugute, indem sie einen Preiskampf verhindert, der die Gewinne verringern würde.

3. Hochfrequenzhandel und Timing von Aufträgen:
   Hochfrequenzhändler (HFTs) konkurrieren oft darum, Aufträge innerhalb von Millisekunden auszuführen, um von kleinen Preisbewegungen zu profitieren. In diesem Wettbewerbsumfeld ist der Algorithmus jedes Händlers darauf ausgelegt, nahezu sofort auf die Aktionen anderer zu reagieren. Wenn eine HFT-Firma versucht, sich zu verlangsamen, um die Genauigkeit zu verbessern, riskiert sie, profitable Trades an schnellere Wettbewerber zu verlieren.

   Nash-Gleichgewicht: Das Gleichgewicht wird erreicht, wenn alle Firmen ähnliche optimierte Algorithmen verwenden, die die Geschwindigkeit maximieren, ohne die Rentabilität zu opfern. Keine einzelne HFT-Firma würde davon profitieren, unilateral langsamer zu werden oder ihren Ansatz zu ändern, da sie im Vergleich zu den Wettbewerbern an Boden verlieren würde. Das Ergebnis ist ein stabiles, schnelles Umfeld, in dem die Strategie jeder Firma durch die Aktionen anderer geprägt ist.

Anwendungen des Nash-Gleichgewichts im Handel

Das Nash-Gleichgewicht hilft Händlern, stabile Punkte im Markt zu verstehen, an denen niemand seine Ergebnisse allein verbessern kann, und bietet wertvolle Einblicke für Strategien. Hier sind einige praktische Anwendungen:

• Identifizierung von Unterstützungs- und Widerstandsniveaus: In Märkten mit großen Akteuren kann das Nash-Gleichgewicht helfen, stabile Preisniveaus vorherzusagen, an denen große Akteure wahrscheinlich ihre Positionen nicht verändern. Dies kann wahrscheinliche Unterstützungs- oder Widerstandspunkte hervorheben und Händlern helfen, Ein- und Ausstiegspreise effektiver festzulegen.

• Optimierung der Handelsgrößen: Durch das Verständnis des Gleichgewichts können Händler große Trades vermeiden, die Preise stören und Reaktionen auslösen könnten. Kleinere, schrittweise Aufträge helfen Händlern, bessere Preise zu erzielen, ohne die Aufmerksamkeit anderer Marktteilnehmer auf sich zu ziehen.

• Navigieren von Market Maker Spreads: Market Maker setzen Geld-Brief-Spannen auf Gleichgewichtsniveaus, um Handelsvolumen und Gewinn auszubalancieren. Das Erkennen dieser Spread-Muster ermöglicht es Händlern, ihre Aufträge zu timen, wenn die Preise stabil sind.

• Antizipieren von Hochfrequenzbewegungen: In schnelllebigen Märkten reagieren Hochfrequenzhändler schnell aufeinander, was Preisstabilität innerhalb enger Spannen schafft. Das Beobachten dieser Gleichgewichtspunkte kann Händlern helfen, Trades in hochliquiden Märkten zu timen.

Die Anwendung des Nash-Gleichgewichts im Handel kann Stabilitätspunkte aufdecken und Händlern helfen, Preisniveaus vorherzusagen und Strategien zu optimieren, die mit dem breiteren Marktverhalten übereinstimmen.

Häufig gestellte Fragen (FAQ)

Was ist das Nash-Gleichgewicht im Handel?

Das Nash-Gleichgewicht im Handel beschreibt einen Punkt, an dem die Strategien der Händler stabil sind, da niemand durch eine alleinige Änderung seiner Vorgehensweise einen Vorteil erlangen kann, gegeben die Strategien der anderen. Es hilft, stabile Preisniveaus und Handelsverhalten in wettbewerbsintensiven Märkten zu erklären.

Wie kann das Nash-Gleichgewicht im Handel genutzt werden?

Händler nutzen das Nash-Gleichgewicht, um Punkte der Marktstabilität vorherzusehen, wie Unterstützungs- und Widerstandsniveaus, an denen die Strategien großer Marktteilnehmer ins Gleichgewicht kommen. Diese Punkte zu erkennen, kann Händlern helfen, effektivere Ein- und Ausstiegspreise festzulegen und Bewegungen zu vermeiden, die den Markt stören könnten.

Ist das Nash-Gleichgewicht in Echtzeit-Handelszenarien anwendbar?

Ja, das Nash-Gleichgewicht ist auf Echtzeit-Handel anwendbar, insbesondere in Märkten mit hohem Volumen, in denen Händler kontinuierlich auf die Bewegungen anderer reagieren. Es ist jedoch entscheidend, Faktoren wie die Marktstimmung und externe Einflüsse zu berücksichtigen, die die Gleichgewichtspunkte beeinflussen können.

Gibt es Alternativen zum Nash-Gleichgewicht in der Handelsanalyse?

Andere Ansätze, wie die Verhaltensspieltheorie und die evolutionäre Spieltheorie, bieten Einblicke in Handelszenarien, in denen Emotionen, Trends oder sich entwickelnde Strategien eine Rolle spielen. Diese können das Nash-Gleichgewicht ergänzen, indem sie Kontext zu Marktverhalten hinzufügen, das möglicherweise nicht strikt stabilen Gleichgewichtsmustern folgt.

Warum ist das Verständnis des Nash-Gleichgewichts für Händler von Vorteil?

Das Beherrschen des Nash-Gleichgewichts hilft Händlern, informierte Entscheidungen zu treffen, indem stabile Preisniveaus identifiziert, Handelszeitpunkte mit Markttrends abgestimmt und disruptive Strategien minimiert werden. Dieses Wissen kann die Fähigkeit eines Händlers verbessern, effektiv durch wettbewerbsintensive und schnelllebige Märkte zu navigieren.

Das Verständnis des Nash-Gleichgewichts kann Händlern einen strategischen Vorteil verschaffen, indem es ihnen hilft, stabile Preisniveaus vorherzusehen und Ein- und Ausstiegspunkte zu optimieren. Die Plattform von Morpher bietet Funktionen, die mit diesem Ansatz übereinstimmen und es Händlern ermöglichen, die Marktinformationen optimal zu nutzen. Mit Echtzeit-Marktdaten, fortgeschrittenen Charting-Tools und handelsgebührenfrei ermöglicht Morpher Ihnen, Strategien basierend auf Gleichgewicht zu erkunden, ohne die typischen Kosten, die den Gewinn schmälern könnten.

Bereit, diese Erkenntnisse in die Tat umzusetzen? Beginnen Sie noch heute mit dem Handel auf Morpher und nutzen Sie eine Plattform, die darauf ausgelegt ist, strategische Handelsentscheidungen zu unterstützen.

Haftungsausschluss: Alle Investitionen sind mit Risiken verbunden und die bisherige Performance eines Wertpapiers, einer Branche, eines Sektors, eines Marktes, eines Finanzprodukts, einer Handelsstrategie oder des Handels einer Einzelperson ist keine Garantie für zukünftige Ergebnisse oder Erträge. Anleger sind voll verantwortlich für alle von ihnen getroffenen Anlageentscheidungen. Solche Entscheidungen sollten ausschließlich auf einer Bewertung ihrer finanziellen Umstände, Anlageziele, Risikobereitschaft und Liquiditätsbedürfnisse basieren. Dieser Beitrag stellt keine Anlageberatung dar