Equilibrio de Nash en el Trading: Encontrando Estabilidad en la Estrategia del Mercado

En el trading, el éxito a menudo depende de anticipar las acciones de otros participantes del mercado. Un concepto poderoso que los traders pueden utilizar para navegar estas dinámicas es el Equilibrio de Nash, un principio de la teoría de juegos donde la estrategia de cada participante es óptima, dadas las elecciones de los demás. Para los traders, el Equilibrio de Nash puede ayudar a explicar cómo se establecen los precios, por qué ciertas operaciones se mantienen estables y cómo realizar movimientos que anticipen las respuestas del mercado.

Consideremos cómo se desarrolla: Cuando los traders toman decisiones como establecer precios de compra o venta, a menudo están reaccionando a o prediciendo lo que otros podrían hacer a continuación. El Equilibrio de Nash describe el momento en que ningún trader individual puede mejorar su resultado cambiando su posición por sí solo. Este concepto permite a los traders comprender mejor los puntos de equilibrio del mercado, ayudándoles a navegar en mercados volátiles, evaluar riesgos e identificar puntos de entrada o salida estables. En este artículo, exploraremos cómo el Equilibrio de Nash puede aplicarse de manera práctica a las estrategias de trading, con ejemplos que llevan esta teoría a un contexto de trading del mundo real.

El Equilibrio de Nash en Breve

El Equilibrio de Nash, nombrado en honor al matemático John Nash, es un concepto clave en la teoría de juegos que describe una situación en la que cada jugador en un "juego" elige la mejor estrategia que puede, dado las estrategias elegidas por los demás. En este punto, ningún jugador puede mejorar su posición cambiando únicamente su propia estrategia: las elecciones de todos están en equilibrio.

El Equilibrio de Nash en la Teoría de Juegos

En la teoría de juegos, el Equilibrio de Nash es el punto donde las estrategias de todos los jugadores se estabilizan, ya que cada persona está tomando la mejor decisión basada en lo que sabe sobre los demás. Este concepto se utiliza ampliamente para predecir el comportamiento en escenarios competitivos donde los resultados dependen de las acciones de múltiples participantes, como en los negocios, la economía y, por supuesto, el trading. El equilibrio ayuda a modelar situaciones en las que cada jugador debe considerar las estrategias de los demás para tomar la mejor decisión posible.

Ejemplos para Ilustrar el Concepto en el Comercio

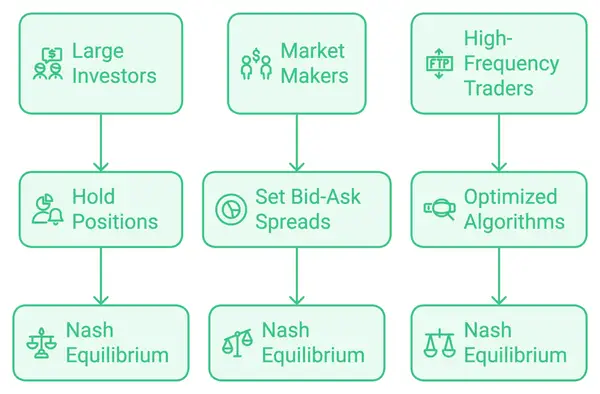
El Equilibrio de Nash juega un papel vital en el comercio, donde los participantes toman decisiones estratégicas basadas en los movimientos esperados de otros. Aquí hay tres ejemplos que muestran cómo se aplica el Equilibrio de Nash a escenarios de comercio:

1. Inversores Grandes y Estabilidad de Precios:
   Imagina a dos grandes inversores que poseen posiciones significativas en una acción en particular. Cada uno sabe que vender una gran parte de sus tenencias probablemente haría que el precio de la acción bajara, afectando sus ganancias. Sin embargo, si ambos traders mantienen sus posiciones, conservan el valor de la acción y evitan una pérdida.

   Equilibrio de Nash: En este caso, ambos traders alcanzan un resultado estable al mantener sus posiciones. Si uno vende mientras el otro mantiene, el vendedor podría experimentar una caída en el precio de sus acciones. En el punto de equilibrio, ninguno de los traders tiene un incentivo para cambiar su estrategia de manera independiente porque hacerlo disminuiría sus ganancias generales.

2. Creadores de Mercado Estableciendo Diferenciales de Compra-Venta:
   Los creadores de mercado son responsables de establecer los precios de compra (bid) y venta (ask) en el mercado. Dos creadores de mercado competidores para el mismo activo deben decidir sobre su diferencial, equilibrando los márgenes de beneficio con el volumen de operaciones. Si uno reduce el diferencial, puede atraer a más traders pero sacrificar ganancias. Si ambos mantienen los diferenciales amplios, el volumen de operaciones podría disminuir debido a los mayores costos para los traders.

   Equilibrio de Nash: El equilibrio ocurre cuando ambos creadores de mercado establecen diferenciales de compra-venta similares que maximizan el beneficio sin sacrificar demasiado volumen. Ninguno puede mejorar su posición solo sin provocar una respuesta del otro, lo que los devolvería a un estado equilibrado. Este diferencial estable beneficia a ambos al prevenir una guerra de precios que reduciría las ganancias.

3. Comercio de Alta Frecuencia y Tiempo de Órdenes:
   Los traders de alta frecuencia (HFT) a menudo compiten para ejecutar órdenes en milisegundos para capitalizar pequeñas fluctuaciones de precios. En este espacio competitivo, el algoritmo de cada trader está diseñado para responder a las acciones de otros casi instantáneamente. Si una firma HFT intenta desacelerar para mejorar la precisión, corre el riesgo de perder operaciones rentables frente a competidores más rápidos.

   Equilibrio de Nash: El equilibrio se alcanza cuando todas las firmas utilizan algoritmos igualmente optimizados que maximizan la velocidad sin sacrificar la rentabilidad. Ninguna firma HFT se beneficiaría al desacelerar unilateralmente o alterar su enfoque, ya que perdería terreno frente a los competidores. El resultado es un entorno estable y de ritmo rápido donde la estrategia de cada firma está moldeada por las acciones de los demás.

Aplicaciones del Equilibrio de Nash en el Comercio

El Equilibrio de Nash ayuda a los traders a comprender los puntos estables en el mercado donde nadie puede mejorar su resultado de manera individual, ofreciendo valiosos conocimientos para la estrategia. A continuación, se presentan algunas aplicaciones prácticas:

• Identificación de Niveles de Soporte y Resistencia: En mercados con grandes participantes, el Equilibrio de Nash puede ayudar a predecir niveles de precios estables donde es poco probable que los grandes jugadores cambien sus posiciones. Esto puede resaltar posibles puntos de soporte o resistencia, ayudando a los traders a establecer precios de entrada y salida de manera más efectiva.

• Optimización de Tamaños de Operaciones: Al comprender el equilibrio, los traders pueden evitar operaciones grandes que podrían alterar los precios y provocar reacciones. Órdenes más pequeñas e incrementales ayudan a los traders a conseguir mejores precios sin atraer la atención de otros participantes del mercado.

• Navegación en los Diferenciales de Creadores de Mercado: Los creadores de mercado establecen diferenciales de compra-venta en niveles de equilibrio para balancear el volumen de operaciones y el beneficio. Reconocer estos patrones de diferencial permite a los traders temporizar sus órdenes cuando los precios son estables.

• Anticipación de Movimientos de Alta Frecuencia: En mercados de rápida evolución, los traders de alta frecuencia reaccionan rápidamente entre sí, creando estabilidad de precios dentro de rangos ajustados. Observar estos puntos de equilibrio puede ayudar a los traders a temporizar las operaciones en mercados altamente líquidos.

Utilizar el Equilibrio de Nash en el comercio puede revelar puntos de estabilidad, ayudando a los traders a anticipar niveles de precios y optimizar estrategias que se alineen con el comportamiento más amplio del mercado.

Preguntas Frecuentes – FAQ

¿Qué es el Equilibrio de Nash en el trading?

El Equilibrio de Nash en el trading describe un punto donde las estrategias de los traders se estabilizan porque nadie puede beneficiarse al cambiar su enfoque por sí solo, dadas las estrategias de los demás. Ayuda a explicar los niveles de precios estables y los comportamientos de trading en mercados competitivos.

¿Cómo se puede utilizar el Equilibrio de Nash en el trading?

Los traders utilizan el Equilibrio de Nash para anticipar puntos de estabilidad del mercado, como niveles de soporte y resistencia, donde las estrategias de los grandes actores se equilibran. Reconocer estos puntos puede ayudar a los traders a establecer precios de entrada y salida más efectivos y evitar movimientos que puedan perturbar el mercado.

¿Es aplicable el Equilibrio de Nash en escenarios de trading en tiempo real?

Sí, el Equilibrio de Nash se aplica al trading en tiempo real, especialmente en mercados de alto volumen donde los traders responden continuamente a los movimientos de los demás. Sin embargo, es crucial considerar factores como el sentimiento del mercado y las influencias externas que pueden afectar los puntos de equilibrio.

¿Existen alternativas al Equilibrio de Nash en el análisis de trading?

Otros enfoques, como la teoría de juegos conductuales y la teoría de juegos evolutivos, ofrecen perspectivas sobre escenarios de trading donde las emociones, tendencias o estrategias en evolución desempeñan un papel. Estos pueden complementar el Equilibrio de Nash al añadir contexto a los comportamientos del mercado que pueden no seguir estrictamente patrones de equilibrio estables.

¿Por qué es beneficioso para los traders entender el Equilibrio de Nash?

Dominar el Equilibrio de Nash ayuda a los traders a tomar decisiones informadas al identificar niveles de precios estables, cronometrar operaciones con las tendencias del mercado y minimizar estrategias disruptivas. Este conocimiento puede mejorar la capacidad de un trader para navegar de manera efectiva en mercados competitivos y de rápido movimiento.

Comprender el Equilibrio de Nash puede ofrecer a los traders una ventaja estratégica, ayudándoles a anticipar niveles de precios estables y optimizar puntos de entrada y salida. La plataforma de Morpher ofrece características que se alinean con este enfoque, permitiendo a los traders aprovechar al máximo los conocimientos del mercado. Con datos de mercado en tiempo real, herramientas de gráficos avanzadas y trading sin comisiones, Morpher te capacita para explorar estrategias basadas en el equilibrio sin los costos típicos que pueden reducir las ganancias.

¿Listo para poner en práctica estos conocimientos? Comienza a operar en Morpher hoy y aprovecha una plataforma diseñada para apoyar decisiones estratégicas de trading.

Descargo de responsabilidad: Todas las inversiones conllevan riesgos y el rendimiento pasado de un valor, industria, sector, mercado, producto financiero, estrategia de trading o trading individual no garantiza resultados o rendimientos futuros. Los inversores son totalmente responsables de cualquier decisión de inversión que tomen. Tales decisiones deben basarse únicamente en una evaluación de sus circunstancias financieras, objetivos de inversión, tolerancia al riesgo y necesidades de liquidez. Esta publicación no constituye asesoramiento de inversión.