Équilibre de Nash dans le Trading : Trouver la Stabilité dans la Stratégie de Marché
Dans le trading, le succès dépend souvent de la capacité à anticiper les actions des autres acteurs du marché. Un concept puissant que les traders peuvent utiliser pour naviguer dans ces dynamiques est l'Équilibre de Nash, un principe de la théorie des jeux où la stratégie de chaque participant est optimale, compte tenu des choix des autres. Pour les traders, l'Équilibre de Nash peut aider à expliquer comment les prix se stabilisent, pourquoi certaines transactions restent constantes et comment effectuer des mouvements qui anticipent les réactions du marché.
Considérez comment cela se déroule : Lorsque les traders prennent des décisions telles que fixer des prix d'achat ou de vente, ils réagissent souvent ou prédisent ce que les autres pourraient faire ensuite. L'Équilibre de Nash décrit le moment où aucun trader unique ne peut améliorer son résultat en changeant sa position seul. Ce concept permet aux traders de mieux comprendre les points d'équilibre du marché, les aidant à naviguer dans des marchés volatils, à évaluer le risque et à identifier des points d'entrée ou de sortie stables. Dans cet article, nous allons explorer comment l'Équilibre de Nash peut être appliqué de manière pratique aux stratégies de trading, avec des exemples qui mettent cette théorie en contexte de trading réel.
L'Équilibre de Nash en Bref
L'Équilibre de Nash, nommé d'après le mathématicien John Nash, est un concept clé de la théorie des jeux qui décrit une situation où chaque joueur dans un "jeu" choisit la meilleure stratégie possible, compte tenu des stratégies choisies par les autres. À ce stade, aucun joueur ne peut améliorer sa position en changeant uniquement sa propre stratégie—les choix de chacun sont en équilibre.
L'Équilibre de Nash dans la Théorie des Jeux
Dans la théorie des jeux, l'Équilibre de Nash est le point où les stratégies de tous les joueurs se stabilisent, chaque personne prenant la meilleure décision basée sur ce qu'elle sait des autres. Ce concept est largement utilisé pour prédire le comportement dans des scénarios compétitifs où les résultats dépendent des actions de plusieurs participants, comme dans les affaires, l'économie et, bien sûr, le trading. L'équilibre aide à modéliser des situations où chaque joueur doit considérer les stratégies des autres pour prendre la meilleure décision possible.
Exemples pour Illustrer le Concept dans le Trading
L'équilibre de Nash joue un rôle essentiel dans le trading, où les participants prennent des décisions stratégiques en fonction des mouvements attendus des autres. Voici trois exemples qui montrent comment l'équilibre de Nash s'applique aux scénarios de trading :
-
Grands Investisseurs et Stabilité des Prix:
Équilibre de Nash: Dans ce cas, les deux traders atteignent un résultat stable en maintenant leurs positions. Si l'un vend tandis que l'autre conserve, le vendeur pourrait connaître une baisse de prix sur ses actions. Au point d'équilibre, aucun des traders n'a de motivation à changer sa stratégie de manière indépendante, car cela réduirait leurs bénéfices globaux.
Imaginez deux grands investisseurs détenant des positions significatives dans une action particulière. Chacun sait que vendre une grande partie de ses avoirs ferait probablement chuter le prix de l'action, affectant ainsi ses bénéfices. Cependant, si les deux traders maintiennent leurs positions, ils préservent la valeur de l'action et évitent une perte. -
Créateurs de Marché Fixant les Spreads d'Offre et de Demande:
Équilibre de Nash: L'équilibre se produit lorsque les deux créateurs de marché fixent des spreads d'offre et de demande similaires qui maximisent les bénéfices sans sacrifier trop de volume. Aucun ne peut améliorer sa position seul sans provoquer une réaction de l'autre, ce qui les ramènerait à un état équilibré. Ce spread stable bénéficie aux deux en empêchant une guerre des prix qui réduirait les bénéfices.
Les créateurs de marché sont responsables de la fixation des prix d'offre (achat) et de demande (vente) sur le marché. Deux créateurs de marché concurrents pour le même actif doivent décider de leur spread, équilibrant les marges bénéficiaires avec le volume des transactions. Si l'un réduit le spread, il peut attirer plus de traders mais sacrifier des bénéfices. Si les deux maintiennent des spreads larges, le volume des transactions pourrait diminuer en raison des coûts plus élevés pour les traders. -
Trading à Haute Fréquence et Timing des Ordres:
Équilibre de Nash: L'équilibre est atteint lorsque toutes les entreprises utilisent des algorithmes optimisés de manière similaire qui maximisent la vitesse sans sacrifier la rentabilité. Aucune entreprise THF ne tirerait profit d'un ralentissement unilatéral ou d'une modification de son approche, car cela la placerait en désavantage par rapport à ses concurrents. Le résultat est un environnement stable et rapide où la stratégie de chaque entreprise est façonnée par les actions des autres.
Les traders à haute fréquence (THF) rivalisent souvent pour exécuter des ordres en quelques millisecondes afin de capitaliser sur de petites fluctuations de prix. Dans cet espace compétitif, l'algorithme de chaque trader est conçu pour répondre aux actions des autres presque instantanément. Si une entreprise THF essaie de ralentir pour améliorer la précision, elle risque de perdre des transactions rentables au profit de concurrents plus rapides.
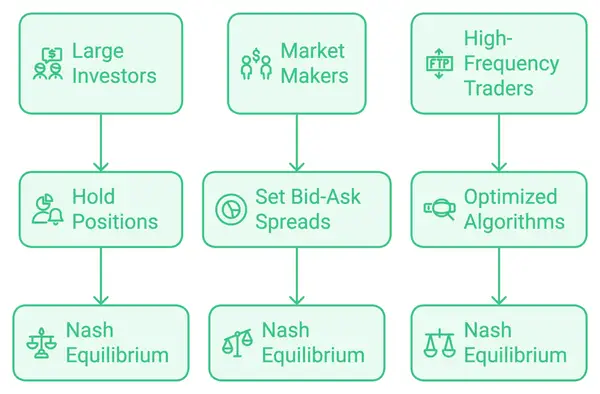
Applications de l'équilibre de Nash dans le trading
L'équilibre de Nash aide les traders à comprendre les points stables sur le marché où personne ne peut améliorer son résultat seul, offrant ainsi des perspectives précieuses pour la stratégie. Voici quelques applications pratiques :
-
Identification des niveaux de support et de résistance : Dans les marchés avec de grands acteurs, l'équilibre de Nash peut aider à prédire les niveaux de prix stables où les grands acteurs sont peu susceptibles de modifier leurs positions. Cela peut mettre en évidence les points de support ou de résistance probables, aidant ainsi les traders à définir plus efficacement leurs prix d'entrée et de sortie.
-
Optimisation des tailles de trade : En comprenant l'équilibre, les traders peuvent éviter de grandes transactions qui pourraient perturber les prix et déclencher des réactions. Des ordres plus petits et progressifs aident les traders à obtenir de meilleurs prix sans attirer l'attention des autres participants du marché.
-
Naviguer dans les spreads des teneurs de marché : Les teneurs de marché fixent les spreads acheteur-vendeur à des niveaux d'équilibre pour équilibrer le volume des transactions et le profit. Reconnaître ces modèles de spread permet aux traders de synchroniser leurs ordres lorsque les prix sont stables.
-
Anticipation des mouvements à haute fréquence : Dans les marchés à mouvement rapide, les traders à haute fréquence réagissent rapidement les uns aux autres, créant une stabilité des prix dans des plages étroites. Observer ces points d'équilibre peut aider les traders à synchroniser leurs transactions dans des marchés très liquides.
Utiliser l'équilibre de Nash dans le trading peut révéler des points de stabilité, aidant les traders à anticiper les niveaux de prix et à optimiser des stratégies qui s'alignent avec le comportement général du marché.
FAQ - Questions Fréquemment Posées
Qu'est-ce que l'Équilibre de Nash en trading ?
L'Équilibre de Nash en trading décrit un point où les stratégies des traders se stabilisent, car personne ne peut en bénéficier en changeant son approche seul, étant donné les stratégies des autres. Cela aide à expliquer les niveaux de prix stables et les comportements de trading dans des marchés compétitifs.
Comment l'Équilibre de Nash peut-il être utilisé en trading ?
Les traders utilisent l'Équilibre de Nash pour anticiper les points de stabilité du marché, tels que les niveaux de support et de résistance, où les stratégies des grands acteurs se équilibrent. Reconnaître ces points peut aider les traders à définir des prix d'entrée et de sortie plus efficaces et à éviter des mouvements qui pourraient perturber le marché.
L'Équilibre de Nash est-il applicable dans des scénarios de trading en temps réel ?
Oui, l'Équilibre de Nash s'applique au trading en temps réel, en particulier dans des marchés à fort volume où les traders réagissent continuellement aux mouvements des autres. Cependant, il est crucial de prendre en compte des facteurs tels que le sentiment du marché et les influences externes qui peuvent impacter les points d'équilibre.
Existe-t-il des alternatives à l'Équilibre de Nash dans l'analyse du trading ?
D'autres cadres, tels que la théorie des jeux comportementaux et la théorie des jeux évolutifs, offrent des perspectives sur des scénarios de trading où les émotions, les tendances ou les stratégies évolutives jouent un rôle. Celles-ci peuvent compléter l'Équilibre de Nash en ajoutant un contexte aux comportements du marché qui peuvent ne pas suivre strictement des modèles d'équilibre stables.
Pourquoi comprendre l'Équilibre de Nash est-il bénéfique pour les traders ?
Maîtriser l'Équilibre de Nash aide les traders à prendre des décisions éclairées en identifiant des niveaux de prix stables, en chronométrant les transactions avec les tendances du marché et en minimisant les stratégies perturbatrices. Cette connaissance peut améliorer la capacité d'un trader à naviguer efficacement dans des marchés compétitifs et rapides.
Comprendre l'Équilibre de Nash peut donner aux traders un avantage stratégique, les aidant à anticiper les niveaux de prix stables et à optimiser les points d'entrée et de sortie. La plateforme de Morpher propose des fonctionnalités qui s'alignent sur cette approche, permettant aux traders de tirer parti des informations du marché. Avec des données de marché en temps réel, des outils de cartographie avancés et un trading sans frais, Morpher vous permet d'explorer des stratégies basées sur l'équilibre sans les coûts habituels qui peuvent réduire les profits.
Prêt à mettre ces connaissances en pratique ? Commencez à trader sur Morpher dès aujourd'hui et profitez d'une plateforme conçue pour soutenir des décisions de trading stratégiques.
Avertissement : Tous les investissements comportent des risques et les performances passées d'un titre, d'un secteur, d'un marché, d'un produit financier, d'une stratégie de trading ou des transactions d'un individu ne garantissent pas les résultats ou les rendements futurs. Les investisseurs sont entièrement responsables de toutes les décisions d'investissement qu'ils prennent. Ces décisions doivent être basées uniquement sur une évaluation de leur situation financière, de leurs objectifs d'investissement, de leur tolérance au risque et de leurs besoins en liquidités. Ce post ne constitue pas un conseil en investissement.

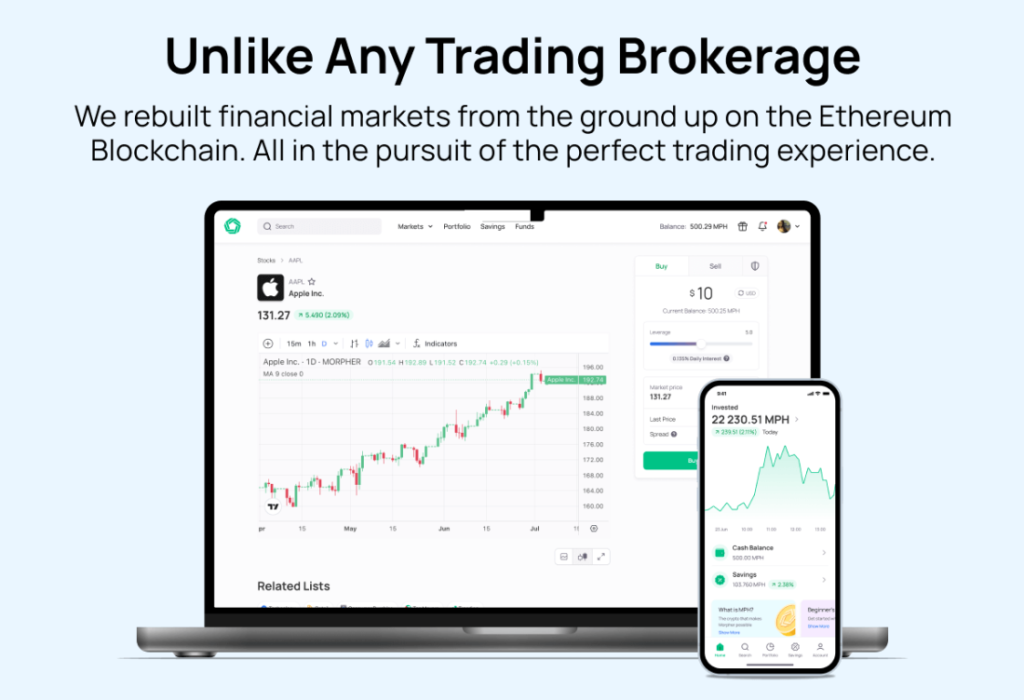
Le trading sans douleur pour tout le monde
Des centaines de marchés en un seul endroit - Apple, Bitcoin, Or, Montres, NFTs, Baskets et bien plus encore.

Le trading sans douleur pour tout le monde
Des centaines de marchés en un seul endroit - Apple, Bitcoin, Or, Montres, NFTs, Baskets et bien plus encore.