Le Modèle de Black-Scholes : Un Guide Pratique pour les Traders d'Options

Le Modèle de Black-Scholes est l'un des outils les plus largement utilisés dans l'évaluation des options, aidant les traders à estimer la juste valeur des contrats d'options. Mais pour beaucoup, sa formule complexe peut sembler intimidante. Dans ce guide, nous allons décomposer le Modèle de Black-Scholes en termes simples, en nous concentrant sur la manière dont vous pouvez l'utiliser dans le trading en conditions réelles.

Que vous négociiez des options sur actions, des devises ou d'autres actifs, le Modèle de Black-Scholes peut vous aider à prendre de meilleures décisions. Nous vous montrerons comment appliquer ce modèle de manière pratique et comment l'utiliser en complément d'autres outils pour obtenir de meilleurs résultats de trading.

Qu'est-ce que le modèle Black-Scholes ?

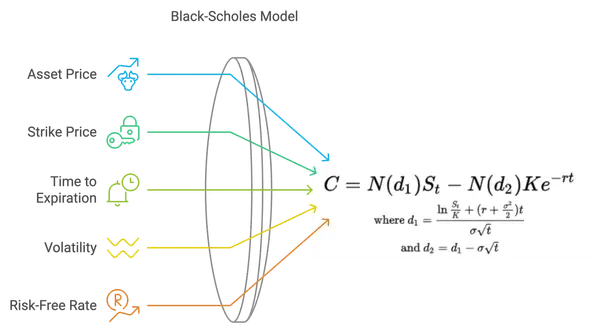
Au fond, le modèle Black-Scholes est un modèle mathématique qui calcule le prix juste d'une option en fonction de cinq facteurs clés : le prix actuel de l'actif, le prix d'exercice de l'option, le temps jusqu'à l'expiration, le taux d'intérêt sans risque, et la volatilité de l'actif.

Composants clés de la formule Black-Scholes

Prix de l'actif : Le prix de marché actuel de l'actif.
Prix d'exercice : Le prix prédéterminé auquel l'option peut être exercée.
Temps jusqu'à l'expiration : La durée restante jusqu'à la date d'expiration de l'option.
Volatilité : La fluctuation attendue du prix de l'actif.
Taux sans risque : Le rendement théorique d'un investissement sans risque, typiquement le rendement des obligations d'État.
En intégrant ces données dans la formule Black-Scholes, vous pouvez calculer le prix théorique de l'option. Mais décomposons cela davantage pour comprendre comment les traders peuvent l'utiliser dans un contexte plus pratique.

Les fondateurs du modèle

Fischer Black et Myron Scholes étaient tous deux des experts dans le domaine de la finance, connus pour leur travail pionnier dans le domaine de la tarification des options. Avec Robert Merton, qui a contribué au développement du modèle, ils ont reçu le Prix Nobel d'économie en 1997.

Black, ancien professeur au MIT, et Scholes, économiste renommé, ont collaboré pour créer un modèle révolutionnaire qui a transformé la manière dont les dérivés financiers sont évalués. Leur approche novatrice pour quantifier le risque et le rendement a ouvert la voie à l'ingénierie financière moderne.

L'objectif principal du modèle

Le modèle Black-Scholes fournit un cadre théorique pour évaluer les options sur la base de certaines hypothèses. En déterminant le prix juste d'une option, il aide les investisseurs à prendre des décisions éclairées concernant l'achat ou la vente d'options. Il joue également un rôle crucial dans les stratégies de gestion des risques.

De plus, l'impact du modèle s'étend au-delà du domaine de la tarification des options. Les traders et les analystes appliquent ses concepts à divers domaines de la finance, notamment pour calculer la volatilité implicite et développer d'autres modèles de tarification des dérivés. Le modèle Black-Scholes témoigne de la puissance de la modélisation mathématique pour comprendre et naviguer dans les complexités des marchés financiers.

Comment le modèle Black-Scholes aide dans le trading réel

Bien que la formule elle-même puisse sembler intimidante, comprendre ce qu'elle fait est relativement simple : elle vous aide à déterminer si une option est surévaluée ou sous-évaluée par rapport au marché. En comparant le prix Black-Scholes avec le prix réel du marché de l'option, vous pouvez prendre des décisions mieux informées concernant l'achat ou la vente.

Imaginez que vous regardez une option d'achat sur une action actuellement cotée à 100 $, avec un prix d'exercice de 105 $, qui expire dans un mois. Vous vous attendez à ce que la volatilité de l'action soit d'environ 20 %, et le taux sans risque actuel est de 1 %. En utilisant le modèle Black-Scholes, vous calculez que le prix juste pour cette option devrait être de 2,50 $. Si le marché évalue l'option à 3,00 $, vous pourriez la considérer comme légèrement surévaluée, ce qui vous donne un aperçu pour vos prises de décision.

Comment utiliser le modèle de Black-Scholes : Guide étape par étape

Voici comment vous pouvez commencer à appliquer le modèle de Black-Scholes dans votre stratégie de trading :

1. Rassembler les données : Vous aurez besoin du prix actuel de l'actif, du prix d'exercice, du temps jusqu'à l'échéance, de la volatilité et du taux sans risque. La plupart des plateformes de trading et des sites financiers fourniront ces valeurs.

2. Utiliser un calculateur de Black-Scholes : Heureusement, vous n'avez pas besoin de résoudre l'équation à la main. Il existe de nombreux calculateurs de Black-Scholes gratuits disponibles en ligne qui peuvent effectuer les calculs pour vous. Il vous suffit d'entrer les valeurs pour calculer le prix de l'option.

3. Comparer avec le prix du marché : Une fois que vous avez le prix selon Black-Scholes, comparez-le avec le prix réel du marché de l'option. L'option est-elle surévaluée ou sous-évaluée ?

4. Effectuer votre trade : Utilisez ces informations en complément d'autres indicateurs et de votre analyse de marché pour décider d'acheter, de vendre ou de conserver votre position sur l'option.

Exemple :

Supposons que le modèle de Black-Scholes évalue une option de vente à 1,50 $, mais que le prix du marché est de 2,00 $. Cela pourrait indiquer que le marché s'attend à une volatilité plus élevée que celle que vous avez calculée, offrant ainsi une opportunité pour vous d'analyser davantage et d'ajuster votre stratégie.

Les Hypothèses Fondamentales du Modèle Black-Scholes

Le Modèle Black-Scholes, une formule révolutionnaire dans le monde de la finance, repose sur plusieurs hypothèses clés qui sont cruciales pour son exactitude et son utilité. Examinons de plus près chacune de ces hypothèses afin de comprendre leur signification dans le contexte de la tarification des options.

Hypothèse des Investisseurs Neutres au Risque

L'une des pierres angulaires du Modèle Black-Scholes est l'hypothèse selon laquelle les investisseurs sont neutres au risque. Cette hypothèse implique que les investisseurs sont indifférents au risque et se concentrent uniquement sur la maximisation de leurs rendements attendus. Bien qu'en réalité, les investisseurs présentent des degrés variés d'aversion au risque, supposer une neutralité au risque simplifie les calculs en permettant l'utilisation de taux d'intérêt sans risque. Cette simplification est essentielle pour l'applicabilité du modèle dans la tarification précise des options et autres dérivés.

Hypothèse de Volatilité Constante

Une autre hypothèse critique du Modèle Black-Scholes est la constance de la volatilité du prix de l'actif sous-jacent. La volatilité, mesure des fluctuations de prix de l'actif, est supposée rester constante durant la durée de vie de l'option. Bien que cette hypothèse ne reflète pas toujours les dynamiques du marché, elle aide à prédire les mouvements de prix futurs et à calculer les rendements attendus. En supposant une volatilité constante, le modèle facilite le processus de valorisation, offrant un cadre plus simple pour la tarification des options.

Hypothèse de Non-Dividence

De plus, le Modèle Black-Scholes fonctionne sous l'hypothèse que l'actif sous-jacent n'émet pas de dividendes durant l'existence de l'option. Bien que cette hypothèse puisse ne pas correspondre à des scénarios du monde réel où les dividendes jouent un rôle significatif dans les décisions d'investissement, elle sert un objectif crucial dans la simplification de la méthodologie de valorisation. En ignorant les paiements de dividendes, le modèle se concentre sur les éléments essentiels de la tarification des options, permettant ainsi une approche plus efficace et standardisée de la valorisation.

Le Cadre Mathématique du Modèle de Black-Scholes

Au cœur du Modèle de Black-Scholes se trouve une équation aux dérivées partielles connue sous le nom d'équation de Black-Scholes. Cette équation relie le prix d'un produit dérivé au prix de l'actif sous-jacent, au temps et à d'autres variables.

Comprendre l'Équation de Black-Scholes

L'équation de Black-Scholes est un modèle en temps continu qui aide à calculer le prix juste des options. Elle prend en compte des facteurs tels que le prix actuel de l'actif sous-jacent, le temps jusqu'à l'expiration, le taux d'intérêt sans risque et la volatilité de l'actif sous-jacent.

Cette équation est dérivée du principe du prix neutre au risque, qui suppose que les investisseurs sont indifférents au risque et exigeront un taux de rendement sans risque pour détenir un actif risqué. En intégrant ces variables dans l'équation, le Modèle de Black-Scholes fournit un cadre mathématique pour déterminer le prix théorique des options sous certaines hypothèses.

Le Rôle de la Distribution Normale

Un concept clé du Modèle de Black-Scholes est l'hypothèse selon laquelle les mouvements de prix de l'actif sous-jacent suivent une distribution log-normale. Cette hypothèse permet l'application de techniques statistiques basées sur la distribution normale, rendant le modèle plus précis et fiable.

En supposant que les prix des actifs suivent une distribution log-normale, le Modèle de Black-Scholes tient compte de l'asymétrie et de l'aplatissement observés sur les marchés financiers. Cette base statistique permet aux traders et aux analystes de prendre des décisions éclairées sur le prix des options et la gestion des risques, améliorant ainsi l'efficacité et l'efficience des marchés financiers.

Limitations du Modèle de Black-Scholes

Bien que le Modèle de Black-Scholes soit largement utilisé, il est important de reconnaître ses limitations :

1. Hypothèse de Volatilité Constante : Le modèle suppose que la volatilité reste constante dans le temps, ce qui n'est pas toujours vrai sur les marchés réels.

2. Aucune Prise en Compte des Dividendes : Si vous tradez des options sur des actions versant des dividendes, le Modèle de Black-Scholes ne prend pas en compte les dividendes sauf s'il est ajusté pour cela.

3. Hypothèse des Options Européennes : Le modèle traite les options comme exerçables uniquement à l'expiration, ce qui le rend idéal pour les options de style européen. Les traders doivent apporter de légers ajustements pour les options américaines, qui permettent l'exercice à tout moment.

Modèle Black-Scholes contre d'autres modèles de tarification des options

Il est utile de comparer le Modèle Black-Scholes avec d'autres modèles de tarification des options, tels que le Modèle Binomial, afin de comprendre quand il peut être plus ou moins approprié.

• Modèle Black-Scholes : Idéal pour les options de style européen et offre une approche rapide et simplifiée.
• Modèle Binomial : Offre plus de flexibilité et peut mieux gérer les options de style américain et la volatilité changeante.

FAQ

Qu'est-ce que le modèle Black-Scholes ?

Le modèle Black-Scholes est une formule mathématique utilisée pour calculer le prix équitable des options. Il prend en compte des facteurs tels que le prix actuel de l'actif sous-jacent, le temps jusqu'à l'expiration, le taux d'intérêt sans risque et la volatilité.

Qui a développé le modèle Black-Scholes ?

Les économistes Fischer Black et Myron Scholes ont développé le modèle Black-Scholes, avec des contributions de Robert Merton. Leur travail leur a valu le prix Nobel d'économie en 1997.

Quelles sont les hypothèses du modèle Black-Scholes ?

Le modèle Black-Scholes suppose des investisseurs neutres au risque, une volatilité constante et l'absence de dividendes versés par l'actif sous-jacent pendant la durée de vie de l'option.

Quelles sont les variables clés du modèle Black-Scholes ?

Les variables clés du modèle Black-Scholes sont le prix de l'action et le prix d'exercice, le temps jusqu'à l'expiration, le taux d'intérêt sans risque et la volatilité. Ces variables jouent un rôle significatif dans la détermination de la valeur des options.

Avec une solide compréhension du modèle Black-Scholes, vous êtes désormais équipé pour naviguer dans le monde du trading d'options en toute confiance. N'oubliez pas de prendre en compte les limitations du modèle et de compléter votre analyse avec d'autres facteurs pour une approche complète du trading. Bon investissement !

Avec votre nouvelle compréhension du modèle Black-Scholes, élevez votre trading d'options à un niveau supérieur en utilisant Morpher. Découvrez l'avenir de l'investissement sur une plateforme qui offre des frais nuls, une liquidité infinie et la possibilité de trader un large éventail d'actifs, des actions aux NFT. Avec Morpher, vous pouvez commencer à investir avec seulement 1 $, profiter d'un effet de levier allant jusqu'à 10x et trader en toute confiance en sachant que vous avez le contrôle total sur vos fonds. Prêt à transformer votre expérience de trading ? Inscrivez-vous et obtenez votre bonus d'inscription gratuit aujourd'hui et rejoignez la révolution sur Morpher.com.

Avertissement : Tous les investissements comportent des risques et les performances passées d'un titre, d'un secteur, d'un marché, d'un produit financier, d'une stratégie de trading ou des transactions d'un individu ne garantissent pas les résultats ou les rendements futurs. Les investisseurs sont entièrement responsables de toutes les décisions d'investissement qu'ils prennent. Ces décisions doivent être basées uniquement sur une évaluation de leur situation financière, de leurs objectifs d'investissement, de leur tolérance au risque et de leurs besoins en liquidités. Ce post ne constitue pas un conseil en investissement.