Todos los artículos 
Anes Bukhdir
Contenido del artículo
El Modelo de Black-Scholes es una de las herramientas más utilizadas en la valoración de opciones, ayudando a los operadores a estimar el valor justo de los contratos de opciones. Pero para muchos, su fórmula compleja puede resultar intimidante. En esta guía, desglosaremos el Modelo de Black-Scholes en términos fáciles de entender, centrándonos en cómo puede utilizarlo en el comercio del mundo real.
Ya sea que esté operando opciones sobre acciones, divisas o otros activos, el Modelo de Black-Scholes puede ayudarle a tomar mejores decisiones. Le mostraremos cómo aplicar este modelo de manera práctica y cómo utilizarlo junto con otras herramientas para obtener mejores resultados en el comercio.
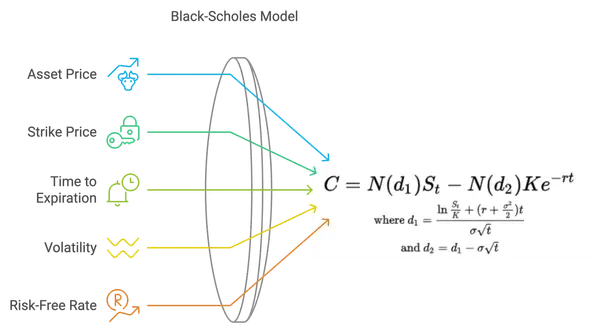
En su esencia, el Modelo de Black-Scholes es un modelo matemático que calcula el precio justo de una opción basado en cinco factores clave: el precio actual del activo, el precio de ejercicio de la opción, el tiempo hasta la expiración, la tasa de interés libre de riesgo y la volatilidad del activo.
Precio del Activo: El precio de mercado actual del activo.
Precio de Ejercicio: El precio predeterminado al cual se puede ejercer la opción.
Tiempo hasta la Expiración: La cantidad de tiempo restante hasta la fecha de expiración de la opción.
Volatilidad: La fluctuación esperada del precio del activo.
Tasa Libre de Riesgo: El rendimiento teórico de una inversión libre de riesgo, típicamente el rendimiento de bonos del gobierno.
Al insertar estos datos en la fórmula de Black-Scholes, se puede calcular el precio teórico de la opción. Pero desglosémoslo más en cómo los traders pueden usarlo en un contexto más práctico.
Fischer Black y Myron Scholes fueron expertos en el campo de las finanzas y conocidos por su trabajo pionero en la fijación de precios de opciones. Junto con Robert Merton, quien contribuyó al desarrollo del modelo, recibieron el Premio Nobel en Ciencias Económicas en 1997.
Black, un ex profesor del MIT, y Scholes, un economista de renombre, colaboraron para crear un modelo innovador que revolucionó la manera en que se valoran los derivados financieros. Su enfoque innovador para cuantificar el riesgo y el rendimiento allanó el camino para la ingeniería financiera moderna.
El Modelo de Black-Scholes proporciona un marco teórico para valorar opciones basado en ciertas suposiciones. Al determinar el precio justo de una opción, ayuda a los inversores a tomar decisiones informadas sobre la compra o venta de opciones. También juega un papel crucial en las estrategias de gestión de riesgos.
Además, el impacto del modelo se extiende más allá del ámbito de la fijación de precios de opciones. Los traders y analistas aplican sus conceptos a diversas áreas de las finanzas, incluida la calculación de la volatilidad implícita y el desarrollo de otros modelos de fijación de precios de derivados. El Modelo de Black-Scholes se erige como un testimonio del poder del modelado matemático en la comprensión y navegación de las complejidades de los mercados financieros.
Aunque la fórmula en sí puede parecer desalentadora, entender qué hace es relativamente simple: ayuda a determinar si una opción está sobrevalorada o subvalorada en comparación con el mercado. Al comparar el precio de Black-Scholes con el precio de mercado real de la opción, se pueden tomar decisiones más informadas sobre si comprar o vender.
Imagina que estás observando una opción de compra sobre una acción que actualmente se cotiza a $100, con un precio de ejercicio de $105, que expira en un mes. Esperas que la volatilidad de la acción sea alrededor del 20%, y la tasa libre de riesgo actual es del 1%. Al utilizar el Modelo de Black-Scholes, calculas que el precio justo para esta opción debería ser $2.50. Si el mercado está valorando la opción en $3.00, podrías considerarla ligeramente sobrevalorada, dándote información valiosa para tu proceso de toma de decisiones.
A continuación, se detalla cómo puede comenzar a aplicar el Modelo Black-Scholes en su estrategia de trading:
Reúna los Datos: Necesitará el precio actual del activo, el precio de ejercicio, el tiempo hasta la expiración, la volatilidad y la tasa libre de riesgo. La mayoría de las plataformas de trading y sitios web financieros proporcionarán estos valores.
Utilice una Calculadora Black-Scholes: Afortunadamente, no necesita resolver la ecuación a mano. Hay muchas calculadoras Black-Scholes gratuitas disponibles en línea que pueden hacer el trabajo por usted. Simplemente ingrese los valores para calcular el precio de la opción.
Compare con el Precio de Mercado: Una vez que tenga el precio Black-Scholes, compárelo con el precio real de mercado de la opción. ¿Está la opción sobrevalorada o subvalorada?
Realice su Operación: Utilice esta información junto con otros indicadores y su análisis de mercado para decidir si comprar, vender o mantener su posición en la opción.
Supongamos que el Modelo Black-Scholes valora una opción de venta en $1.50, pero el precio de mercado es $2.00. Esto podría indicar que el mercado espera una mayor volatilidad de la que usted ha calculado, brindándole una oportunidad para analizar más a fondo y ajustar su estrategia.
El Modelo Black-Scholes, una fórmula innovadora en el mundo de las finanzas, se basa en varias suposiciones clave que son fundamentales para su precisión y utilidad. Profundicemos en cada una de estas suposiciones para entender su importancia en el contexto de la valoración de opciones.
Una de las piedras angulares del Modelo Black-Scholes es la suposición de que los inversores son neutros al riesgo. Esta suposición implica que los inversores son indiferentes al riesgo y se centran únicamente en maximizar sus rendimientos esperados. Aunque en la realidad, los inversores muestran diferentes grados de aversión al riesgo, asumir la neutralidad al riesgo simplifica los cálculos al permitir el uso de tasas de interés libres de riesgo. Esta simplificación es esencial para la aplicabilidad del modelo en la valoración precisa de opciones y otros derivados.
Otra suposición crítica del Modelo Black-Scholes es la constancia de la volatilidad en el precio del activo subyacente. La volatilidad, una medida de las fluctuaciones del precio del activo, se asume que permanece constante durante la vida de la opción. Esta suposición, aunque no siempre refleja la dinámica del mercado, ayuda a predecir movimientos futuros de precios y a calcular rendimientos esperados. Al asumir volatilidad constante, el modelo simplifica el proceso de valoración, proporcionando un marco más directo para la fijación de precios de opciones.
Además, el Modelo Black-Scholes opera bajo la suposición de que el activo subyacente no emite dividendos durante la existencia de la opción. Si bien esta suposición puede no alinearse con escenarios del mundo real en los que los dividendos juegan un papel significativo en las decisiones de inversión, cumple una función crucial al simplificar la metodología de valoración. Al despreciar los pagos de dividendos, el modelo se centra en los elementos centrales de la valoración de opciones, permitiendo un enfoque más eficiente y estandarizado para la valoración.
En el corazón del Modelo Black-Scholes se encuentra una ecuación en derivadas parciales conocida como la ecuación de Black-Scholes. Esta ecuación relaciona el precio de un activo derivado con el precio del activo subyacente, el tiempo y otras variables.
La ecuación de Black-Scholes es un modelo de tiempo continuo que ayuda a calcular el precio justo de las opciones. Toma en cuenta factores como el precio actual del activo subyacente, el tiempo hasta el vencimiento, la tasa de interés libre de riesgo y la volatilidad del activo subyacente.
Esta ecuación se deriva del principio de valoración neutral al riesgo, que supone que los inversores son indiferentes al riesgo y requerirán una tasa de retorno libre de riesgo para mantener un activo arriesgado. Al incorporar estas variables en la ecuación, el Modelo Black-Scholes proporciona un marco matemático para determinar el precio teórico de las opciones bajo ciertas suposiciones.
Un concepto clave en el Modelo Black-Scholes es la suposición de que los movimientos de precios del activo subyacente siguen una distribución log-normal. Esta suposición permite la aplicación de técnicas estadísticas basadas en la distribución normal, haciendo que el modelo sea más preciso y confiable.
Al asumir que los precios de los activos siguen una distribución log-normal, el Modelo Black-Scholes toma en cuenta la asimetría y la curtosis observadas en los mercados financieros. Esta base estadística permite a los operadores y analistas tomar decisiones informadas sobre la valoración de opciones y la gestión del riesgo, mejorando la eficiencia y efectividad de los mercados financieros.
Aunque el Modelo Black-Scholes se utiliza ampliamente, es importante reconocer sus limitaciones:
Suposición de Volatilidad Constante: El modelo asume que la volatilidad permanece constante en el tiempo, lo cual no siempre es cierto en los mercados reales.
No Considera los Dividendos: Si está operando opciones sobre acciones que pagan dividendos, el Modelo Black-Scholes no tiene en cuenta los dividendos a menos que se ajuste para ello.
Suposición de Opciones Europeas: El modelo trata las opciones como ejercitables solo al vencimiento, lo que lo hace ideal para opciones de estilo europeo. Los operadores deben hacer ligeros ajustes para las opciones americanas, que permiten el ejercicio en cualquier momento.
Es útil comparar el Modelo de Black-Scholes con otros modelos de valoración de opciones, como el Modelo Binomial, para entender cuándo puede ser más o menos adecuado.
El Modelo Black-Scholes es una fórmula matemática utilizada para calcular el precio justo de las opciones. Tiene en cuenta factores como el precio actual del activo subyacente, el tiempo hasta el vencimiento, la tasa de interés libre de riesgo y la volatilidad.
Los economistas Fischer Black y Myron Scholes desarrollaron el Modelo Black-Scholes, con contribuciones de Robert Merton. Su trabajo les valió el Premio Nobel en Ciencias Económicas en 1997.
El Modelo Black-Scholes supone inversores neutrales al riesgo, volatilidad constante y que no se pagan dividendos por el activo subyacente durante la vida de la opción.
Las variables clave en el Modelo Black-Scholes son el precio de la acción y el precio de ejercicio, el tiempo hasta el vencimiento, la tasa de interés libre de riesgo y la volatilidad. Estas variables juegan un papel significativo en la determinación del valor de las opciones.
Con una comprensión sólida del Modelo Black-Scholes, ahora está preparado para navegar por el mundo del comercio de opciones con confianza. Recuerde considerar las limitaciones del modelo y complementar su análisis con otros factores para un enfoque integral en el comercio. ¡Felices inversiones!
Con su nuevo entendimiento del Modelo Black-Scholes, eleve su comercio de opciones al siguiente nivel utilizando Morpher. Experimente el futuro de la inversión en una plataforma que ofrece cero comisiones, liquidez infinita y la capacidad de negociar una amplia variedad de activos, desde acciones hasta NFT. Con Morpher, puede comenzar a invertir con solo $1, disfrutar de un apalancamiento de hasta 10 veces y operar con confianza sabiendo que tiene el control total de sus fondos. ¿Listo para transformar su experiencia de comercio? Regístrese y obtenga su bono de registro gratuito hoy y únase a la revolución en Morpher.com.
Descargo de responsabilidad: Todas las inversiones conllevan riesgos y el rendimiento pasado de un valor, industria, sector, mercado, producto financiero, estrategia de trading o trading individual no garantiza resultados o rendimientos futuros. Los inversores son totalmente responsables de cualquier decisión de inversión que tomen. Tales decisiones deben basarse únicamente en una evaluación de sus circunstancias financieras, objetivos de inversión, tolerancia al riesgo y necesidades de liquidez. Esta publicación no constituye asesoramiento de inversión.
Comercio sin complicaciones para todos
Cientos de mercados en un solo lugar - Apple, Bitcoin, Oro, Relojes, NFTs, Zapatillas y mucho más.
Comercio sin complicaciones para todos
Cientos de mercados en un solo lugar - Apple, Bitcoin, Oro, Relojes, NFTs, Zapatillas y mucho más.
