Was ist R-Quadrat? Ein Leitfaden zum Bestimmtheitsmaß

Als statistischer Analyst kann ich die Bedeutung des Verständnisses und der Nutzung von R-Quadrat (R²) in der statistischen Analyse nicht genug betonen. Sie spielen eine entscheidende Rolle in der Regressionsanalyse, indem sie zeigen, wie gut ein Modell zu den Daten passt. Im Wesentlichen beantworten sie die Frage: Wie viel der Variation des Ergebnisses kann durch die Prädiktoren erklärt werden?

In diesem Artikel werde ich Sie durch das Konzept von R-Quadrat führen, seine Rolle in der statistischen Analyse, seine Interpretation, Einschränkungen und wie es mit dem bereinigten R-Quadrat verbessert werden kann. Wenn Sie also bereit sind, Ihre statistische Analyse auf das nächste Level zu heben, lassen Sie uns gleich eintauchen!

Was ist R-Quadrat (R²) oder der Bestimmtheitsfaktor?

R-Quadrat, oder der Bestimmtheitsfaktor, misst den Anteil der Varianz der abhängigen Variable, der durch unabhängige Variablen in einem Regressionsmodell erklärt werden kann.

Einfach ausgedrückt zeigt es, wie gut Ihr Modell zu den Daten passt.

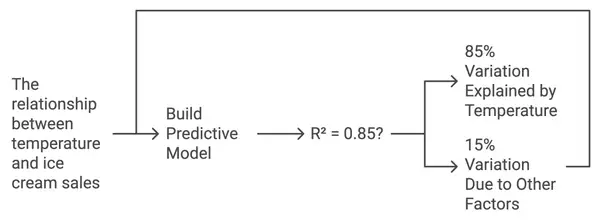
Als Ausgangspunkt nehmen wir an, Sie analysieren die Beziehung zwischen Temperatur und Eism Verkaufszahlen. Sie erstellen ein Modell, um die Verkäufe basierend auf der Temperatur vorherzusagen. Wenn der R²-Wert 0,85 (oder 85%) beträgt, bedeutet dies, dass 85% der Variation der Eism Verkaufszahlen durch Veränderungen der Temperatur erklärt werden können. Die verbleibenden 15% könnten auf andere Faktoren zurückzuführen sein, wie beispielsweise Werbeaktionen oder Wetterbedingungen.

R² (Bestimmtheitsmaß) Werte

• R² = 1: Eine perfekte Anpassung. Das Modell erklärt 100% der Variabilität der abhängigen Variablen.
• R² = 0: Keine erklärende Kraft. Das Modell berücksichtigt keine Variation in der abhängigen Variablen.
• Zwischenwerte (z. B. 0,4 oder 0,7): Diese deuten auf eine partielle Anpassung hin. Ein R² von 0,7 bedeutet zum Beispiel, dass 70% der Varianz durch das Modell erklärt werden und 30% unerklärt bleiben.

Höhere R²-Werte bedeuten in der Regel eine bessere Modellanpassung, garantieren jedoch keine Genauigkeit oder Kausalität. Der Kontext ist entscheidend: Ein hoher R²-Wert in einem Bereich (wie der Physik) könnte erwartet werden, während niedrigere Werte in Bereichen mit höherer Variabilität (wie den Sozialwissenschaften) dennoch akzeptabel sein könnten.

Die Mathematische Formel von R Quadrat

R² wird berechnet als:

R² = 1 – (SSE / SST)

• SSE (Summe der quadrierten Fehler): Misst die Abweichung zwischen beobachteten und vorhergesagten Werten.
• SST (Gesamtsumme der Quadrate): Erfasst die gesamte Variabilität in den Daten im Vergleich zum Mittelwert.

Beispielrechnung

Stellen Sie sich ein Modell vor, das monatliche Verkaufszahlen vorhersagt:

• SST (gesamte Variabilität) = 1000.
• SSE (nicht erklärte Variabilität) = 300.

R² = 1 – (300 / 1000) = 0.7

Das bedeutet, dass das Modell 70% der Variabilität der Verkaufszahlen erklärt.

R-Quadrat im Handel

Im Handel kann R² Ihnen helfen zu bewerten, wie gut bestimmte Faktoren oder Indikatoren die Bewegungen des Preises eines Vermögenswerts erklären. Durch den Aufbau von Regressionsmodellen können Sie die Stärke der Beziehungen zwischen Variablen bewerten, wie zum Beispiel:

• Marktindizes und Aktienperformance.
• Wirtschaftliche Indikatoren (z. B. Zinssätze, Inflation) und Währungswerte.
• Technische Indikatoren (z. B. gleitende Durchschnitte, RSI) und Preisänderungen von Vermögenswerten.

Wenn Sie beispielsweise R² verwenden, um zu analysieren, wie der Preis einer Aktie mit dem breiteren Marktindex korreliert, zeigt ein hohes R² (z. B. 0,8), dass 80 % der Preisbewegungen der Aktie durch den Index erklärt werden. Dies deutet auf eine starke Beziehung hin, die nützlich für Strategien wie marktneutrales Handeln oder Beta-Hedging ist.

Mit Morpher können Sie Ihre Strategien in einer risikofreien Umgebung testen, ohne Gebühren handeln, detaillierte technische Charts überprüfen und nahtlos auf globale Märkte zugreifen. Beginnen Sie jetzt mit dem Testen auf Morpher!

A

Das adjustierte R² verbessert das standardmäßige R², indem es die Anzahl der Prädiktoren im Modell berücksichtigt und unnötige Komplexität bestraft. Dies stellt sicher, dass das Hinzufügen zusätzlicher Variablen die Kennzahl nicht künstlich erhöht, ohne eine sinnvolle Verbesserung der Modellleistung zu bewirken.

Wie das adjustierte R² funktioniert

Die Formel für das adjustierte R² berücksichtigt sowohl die Gesamtanzahl der Prädiktoren als auch die Stichprobengröße:

Adjustiertes R² = 1 - ((n - 1) * (1 - R²)) / (n - k - 1)

Wo:

• R-Quadrat: Der standardmäßige Bestimmtheitsmaß.
• n: Gesamtanzahl der Beobachtungen (Stichprobengröße).
• k: Anzahl der Prädiktoren (unabhängige Variablen) im Modell.

Diese Verfeinerung macht das adjustierte R² besonders wertvoll, wenn Modelle mit unterschiedlichen Anzahl von Prädiktoren verglichen werden. Ein besseres Modell hat ein höheres adjustiertes R², während irrelevante Prädiktoren es verringern.

Beispielberechnung

Stellen Sie sich ein Modell vor, bei dem:

• R-Quadrat: 0,85
• n=100 (Beobachtungen)
• k=3 (Prädiktoren)

Adjustiertes R² = 1 − ((1 − 0,85) ⋅ (100 − 1)) / (100 − 3 − 1) Adjustiertes R² = 1 − ((0,15 ⋅ 99) / 96) Adjustiertes R² = 1 − 0,1547 Adjustiertes R² = 0,8453

Wenn das adjustierte R² sinkt, wenn ein Prädiktor hinzugefügt wird, ist das ein Zeichen dafür, dass die Variable das Modell nicht sinnvoll verbessert. Dies hilft, Überanpassung zu verhindern und das Modell einfacher zu halten.

Vergleich von R² und Adjusted R² in der Praxis

Wann R-Quadrat irreführend sein kann: Einschränkungen

Obwohl R² wertvoll ist, hat es seine Einschränkungen:

• Kausalität: R² misst nur die Korrelation, nicht die Kausalität. Ein hohes R² impliziert nicht, dass eine Variable Veränderungen in einer anderen verursacht.
• Ausreißer und Multikollinearität: Extreme Werte oder hoch korrelierte Prädiktoren können R² verzerren.
• Nicht-lineare Beziehungen: R² funktioniert nicht gut für nicht-lineare Modelle, bei denen die Beziehungen keine geraden Linien sind.

Häufig gestellte Fragen zu R-Quadrat

Was stellt R² in der Regression dar?

R² misst, wie viel der Varianz der abhängigen Variablen durch die unabhängigen Variablen erklärt wird.

Wie interpretiere ich den Bestimmtheitsmaß (R²)?

Höhere Werte (näher an 1) weisen auf eine bessere Modellanpassung hin, während niedrigere Werte darauf hindeuten, dass das Modell nicht viel Varianz erklärt.

Was ist der Unterschied zwischen R² und angepasstem R²?

Das angepasste R² bestraft Modelle für unnötige Prädiktoren und bietet ein genaueres Maß beim Vergleich von Modellen.

Wann sollte ich das angepasste R² verwenden?

Wenn Sie es mit Modellen zu tun haben, die mehrere Prädiktoren enthalten, oder beim Vergleich von Modellen unterschiedlicher Komplexität.

Fazit

R² und adjustiertes R² sind leistungsstarke Werkzeuge zum Verständnis und zur Verfeinerung von Regressionsmodellen. R² misst, wie gut Ihr Modell zu den Daten passt, während adjustiertes R² sicherstellt, dass Komplexität nicht auf Kosten der Genauigkeit geht.

Durch die Integration dieser Kennzahlen in Ihr statistisches Werkzeugset können Sie stärkere, zuverlässigere Modelle erstellen und tiefere Einblicke in Ihre Daten gewinnen.

Wenn Sie bereit sind, Ihre Datenanalysefähigkeiten auf die nächste Ebene zu heben, warum wenden Sie diese Erkenntnisse nicht im Handel an?

Bei Morpher können Sie intelligenter investieren mit null Gebühren, unendlicher Liquidität und innovativen Tools. Beginnen Sie noch heute mit der Erkundung von Morpher!

Haftungsausschluss: Alle Investitionen sind mit Risiken verbunden, und die vergangene Performance eines Wertpapiers, einer Branche, eines Sektors, eines Marktes, eines Finanzprodukts, einer Handelsstrategie oder des Handels einer Einzelperson garantiert keine zukünftigen Ergebnisse oder Renditen. Investoren sind vollständig verantwortlich für alle Investitionsentscheidungen, die sie treffen. Solche Entscheidungen sollten ausschließlich auf einer Bewertung ihrer finanziellen Verhältnisse, Anlageziele, Risikotoleranz und Liquiditätsbedürfnisse basieren. Dieser Beitrag stellt keine Anlageberatung dar.