The Concept of Chain Abstraction

Chain abstraction is a fascinating concept that has gained significant attention in various fields, from computer science to mathematics. In this article, we will delve into the intricate details of chain abstraction, exploring its definition, theoretical framework, application in different fields, the process involved, and its impact on problem-solving.

Understanding Chain Abstraction: A Brief Overview

Before we dive into the depths of chain abstraction, let’s take a moment to grasp its essence in a nutshell. Chain abstraction can be defined as the process of simplifying complex systems or problems by breaking them down into a series of interconnected elements or links. These links form a chain, where each element contributes to the overall understanding of the system or problem at hand.

Chain abstraction is akin to unraveling a tangled web of information, revealing the underlying structure and connections that may not be immediately apparent. It is a methodical approach that allows us to navigate through intricate concepts with clarity and precision, much like following a trail of breadcrumbs through a dense forest.

Defining Chain Abstraction

In its core essence, chain abstraction involves the decomposition of complex structures or phenomena into smaller, interconnected components. By dissecting a system or problem into its fundamental building blocks, chain abstraction facilitates a more comprehensive analysis and understanding of the intricate relationships between these elements.

Imagine a complex puzzle being deconstructed into individual pieces, each with its unique shape and role in the grand scheme of things. Chain abstraction serves as a mental toolkit that helps us organize these pieces in a logical sequence, allowing us to see the bigger picture and how each piece fits into the puzzle.

The Importance of Chain Abstraction

Chain abstraction plays a pivotal role in various fields, including computer science, mathematics, and even everyday problem-solving. By simplifying complex systems, it enables us to identify patterns, relationships, and dependencies that may not be evident at first glance. This abstraction process empowers us to tackle complex problems more efficiently and develop effective strategies for finding solutions.

Moreover, chain abstraction fosters a holistic perspective, encouraging us to view problems from multiple angles and consider the interconnectedness of various factors. It prompts us to think beyond the surface level and delve deeper into the underlying structures that govern the behavior of systems and phenomena.

The Theoretical Framework of Chain Abstraction

Now that we comprehend the basics of chain abstraction let’s explore its theoretical framework and key principles that underpin this fascinating concept.

Chain abstraction, a fundamental concept in systems thinking and problem-solving methodologies, delves into the intricate web of relationships that exist within complex systems. Beyond just a surface-level analysis, chain abstraction delves deep into the core of interconnected elements, unraveling the hidden dynamics that drive the functioning of a system. It goes beyond the mere identification of components to reveal the underlying dependencies and interactions that shape the system’s behavior.

Key Principles and Concepts

At its core, chain abstraction relies on the interplay of several key principles and concepts. These include the identification of system elements, determining their relationships and dependencies, and understanding how they collectively contribute to the overall system or problem. By analyzing these linkages, we can uncover hidden connections and gain insights that may otherwise be overlooked.

Furthermore, chain abstraction emphasizes the holistic view of a system, highlighting the importance of considering not just individual components but also their interconnectedness. This interconnectedness forms the basis of emergent properties, where the system as a whole exhibits behaviors and characteristics that are not present in its individual parts. Understanding and leveraging these emergent properties are crucial in harnessing the full potential of chain abstraction.

The Evolution of Chain Abstraction Theory

Over time, chain abstraction theory has evolved, adapting and expanding to cater to the specific needs of various fields. This ongoing evolution showcases the versatility and significance of this approach and its far-reaching applicability across disciplines.

As different industries and domains recognize the value of systems thinking and interconnected problem-solving, chain abstraction continues to evolve, incorporating insights and methodologies from diverse fields. This adaptability and openness to interdisciplinary collaboration underscore the robustness of chain abstraction theory and its ability to transcend traditional boundaries.

Chain Abstraction in Different Fields

Chain abstraction finds applications in diverse areas, proving its relevance beyond theoretical frameworks. Let’s explore its significance in computer science, mathematics, and beyond.

Chain Abstraction in Computer Science

In the realm of computer science, chain abstraction aids in simplifying complex algorithms and data structures. By breaking them down into manageable components, it enhances our understanding of computational processes and helps improve their efficiency and performance.

Moreover, chain abstraction in computer science is not limited to algorithmic optimization. It also plays a crucial role in software engineering, where it facilitates the design and implementation of modular and scalable systems. This approach allows developers to create robust and maintainable codebases, leading to more reliable software products.

Chain Abstraction in Mathematics

In mathematics, chain abstraction assists in tackling intricate problems by providing a systematic approach to dissect and analyze complex mathematical structures. It helps mathematicians explore relationships and patterns, leading to breakthroughs in various branches of the discipline.

Furthermore, the application of chain abstraction in mathematics extends to fields such as cryptography and number theory. By leveraging the principles of chain abstraction, experts in these domains can develop secure encryption schemes and solve challenging mathematical puzzles that underpin modern cybersecurity protocols.

The Process of Chain Abstraction

Now that we’ve explored the concepts and applications of chain abstraction in different fields let’s delve into the process involved in effectively utilizing this powerful strategy.

Chain abstraction is a systematic and structured approach that plays a crucial role in understanding complex systems and problems. By breaking down intricate systems into manageable components, chain abstraction allows for a detailed analysis of the relationships and interactions between these elements. This method not only aids in problem-solving but also provides valuable insights into the underlying mechanisms governing the system’s behavior.

Steps Involved in Chain Abstraction

The process of chain abstraction typically comprises several steps, including identifying the system or problem, disaggregating it into its constituent elements, analyzing the relationships between these elements, and constructing a coherent chain that depicts their interdependencies. This systematic approach enables us to gain a holistic understanding of the system or problem, facilitating effective problem-solving.

Moreover, each step in the chain abstraction process is essential for creating a comprehensive overview of the system’s structure and dynamics. From defining the boundaries of the system to evaluating the feedback loops within the chain, every detail contributes to a more nuanced understanding of the system’s behavior and potential points of intervention.

Tools and Techniques for Chain Abstraction

Various tools and techniques assist in the process of chain abstraction. These include graphical representations, such as flowcharts and mind maps, which visually depict the links between system elements. Additionally, software tools designed specifically for chain abstraction can streamline the process, supporting the analysis and visualization of complex chains.

Furthermore, the use of qualitative and quantitative methods alongside these tools enhances the accuracy and depth of the chain abstraction process. By incorporating data-driven insights and statistical analyses, practitioners can uncover patterns and trends within the system, leading to more informed decision-making and strategic planning.

The Impact of Chain Abstraction on Problem Solving

Chain abstraction has a profound impact on problem-solving, enabling us to approach complex problems with clarity and efficiency. Let’s explore some key ways in which chain abstraction enhances our cognitive abilities and facilitates complex problem-solving.

Enhancing Cognitive Abilities

By breaking complex problems into manageable components, chain abstraction enhances our cognitive abilities, allowing us to focus on specific elements without being overwhelmed by the overall complexity. This targeted approach improves our capacity to process information, make connections, and generate innovative solutions.

Facilitating Complex Problem Solving

Complex problems often require a structured and systematic approach, and chain abstraction provides just that. By revealing the underlying relationships and dependencies, it enables us to identify critical factors, prioritize actions, and develop effective strategies to tackle multifaceted problems. The application of chain abstraction fosters a methodical problem-solving mindset that can lead to successful outcomes.

FAQ

What is chain abstraction?

Chain abstraction is the process of simplifying complex systems or problems by breaking them down into interconnected elements or links, forming a chain. It enables a more comprehensive understanding of the system or problem at hand.

Where is chain abstraction used?

Chain abstraction finds applications in various fields, including computer science, mathematics, and everyday problem-solving. It assists in simplifying complex algorithms, data structures, and mathematical problems.

What are the key steps in the process of chain abstraction?

The process of chain abstraction involves identifying the system or problem, disaggregating it into its constituent elements, analyzing their relationships, and constructing a coherent chain that shows their interdependencies. This systematic approach facilitates effective problem-solving.

How does chain abstraction enhance problem-solving?

Chain abstraction enhances problem-solving by breaking down complex problems into manageable components, improving cognitive abilities, and facilitating a structured and systematic approach. It enables us to identify critical factors, prioritize actions, and develop effective strategies for tackling complex problems.

What tools are available for chain abstraction?

Various tools and techniques can aid in the process of chain abstraction, including graphical representations like flowcharts and mind maps. Software tools designed specifically for chain abstraction can also assist in the analysis and visualization of complex chains.

Does chain abstraction have real-world applications?

Yes, chain abstraction has real-world applications beyond theoretical frameworks. It finds practical utility in fields like computer science and mathematics, where it aids in simplifying complex systems and developing efficient strategies for problem-solving.

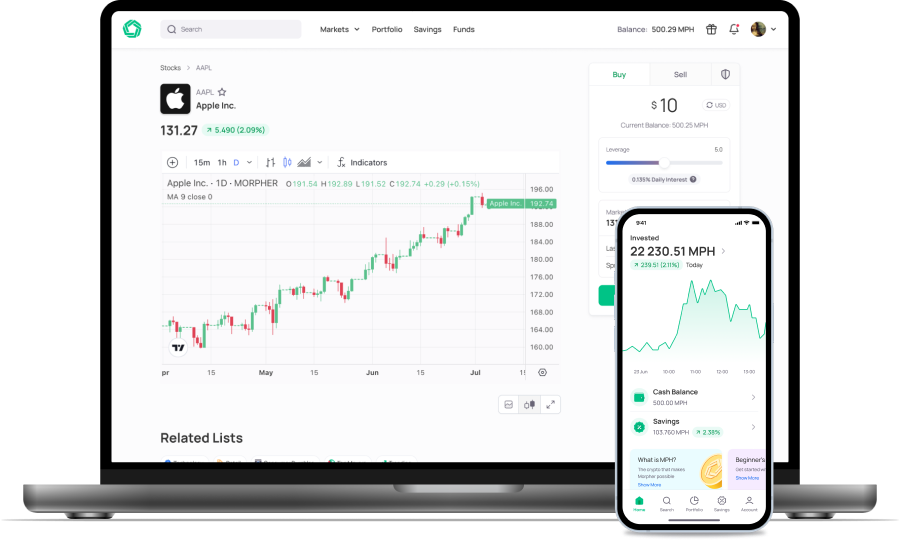
As we’ve explored the concept of chain abstraction and its profound impact on problem-solving across various fields, it’s clear that innovative approaches are essential in navigating complex systems. Morpher.com embodies this spirit of innovation by transforming the world of investing through blockchain technology. With its zero fees, infinite liquidity, fractional investing, and unique trading experience, Morpher is the perfect platform for those seeking to apply systematic strategies in the financial markets. Ready to take your trading to the next level with Morpher’s revolutionary platform? Sign Up and Get Your Free Sign Up Bonus today and join the future of investing.

Disclaimer: All investments involve risk, and the past performance of a security, industry, sector, market, financial product, trading strategy, or individual’s trading does not guarantee future results or returns. Investors are fully responsible for any investment decisions they make. Such decisions should be based solely on an evaluation of their financial circumstances, investment objectives, risk tolerance, and liquidity needs. This post does not constitute investment advice.